Haiyang Yu's Blog

Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

1
2
3
4
5
6
7

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

Return:

1
2
3
4

[
   [5,4,11,2],
   [5,8,4,5]
]

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

1
2
3
4
5
6
7

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

Given two integers n and k, return all possible combinations of k numbers out of 1 … n.

You may return the answer in any order.

Example 1:

1
2
3
4
5
6
7
8
9
10

Input: n = 4, k = 2
Output:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

Example 2:

1
2

Input: n = 1, k = 1
Output: [[1]]

Constraints:

• 1 <= n <= 20
• 1 <= k <= n

Given an m x n 2d grid map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

1
2
3
4
5
6
7

Input: grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
Output: 1

Example 2:

1
2
3
4
5
6
7

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] is '0' or '1'.

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

1
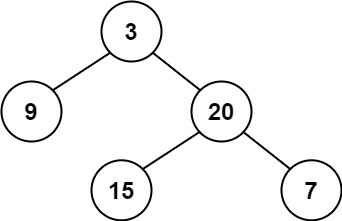
2

Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

1
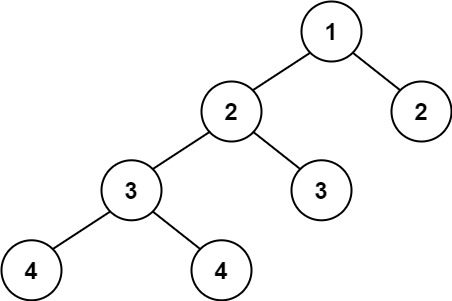
2

Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

1
2

Input: root = []
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -104 <= Node.val <= 104

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example 1:

1
2
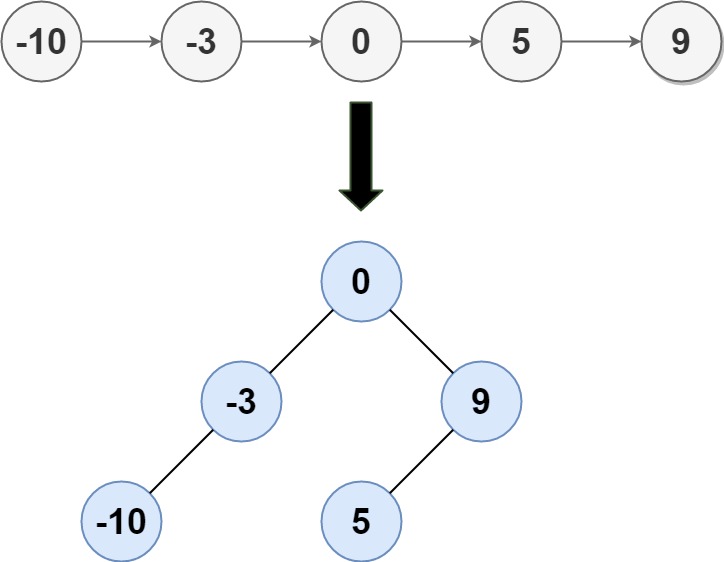
3

Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

1
2

Input: head = []
Output: []

Example 3:

1
2

Input: head = [0]
Output: [0]

Example 4:

1
2

Input: head = [1,3]
Output: [3,1]

Constraints:

• The number of nodes in head is in the range [0, 2 * 104].
• -10^5 <= Node.val <= 10^5

Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1 … n.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Input: 3
Output:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

Constraints:

• 0 <= n <= 8

There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station’s index if you can travel around the circuit once in the clockwise direction, otherwise return -1.

Note:

• If there exists a solution, it is guaranteed to be unique.
• Both input arrays are non-empty and have the same length.
• Each element in the input arrays is a non-negative integer.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Input: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

Output: 3

Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13

Input: 
gas  = [2,3,4]
cost = [3,4,3]

Output: -1

Explanation:
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.

Given two arrays, write a function to compute their intersection.

Example 1:

1
2

Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2]

Example 2:

1
2

Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output: [9,4]

Note:

• Each element in the result must be unique.
• The result can be in any order.

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

1
2
3
4
5
6

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

• You may only use constant extra space.
• Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

1
2
3

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

• The number of nodes in the given tree is less than 4096.
• -1000 <= node.val <= 1000