Haiyang Yu's Blog
0%

Leetcode 145 Binary Tree Postorder Traversal

发表于 更新于 分类于 Valine：
本文字数： 1.9k 阅读时长 ≈ 2 分钟

Given the root of a binary tree, return the postorder traversal of its nodes’ values.

Example 1:

img

1
2
Input: root = [1,null,2,3]
Output: [3,2,1]

Example 2:

1
2
Input: root = []
Output: []

Example 3:

1
2
Input: root = [1]
Output: [1]

Example 4:

img

1
2
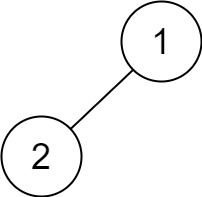
Input: root = [1,2]
Output: [2,1]

Example 5:

img

1
2
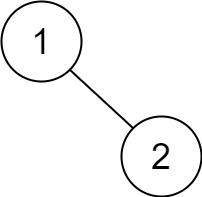
Input: root = [1,null,2]
Output: [2,1]

Constraints:

  • The number of the nodes in the tree is in the range [0, 100].
  • -100 <= Node.val <= 100

Follow up:

Recursive solution is trivial, could you do it iteratively?

非递归

参考于https://www.cnblogs.com/mini-coconut/p/9079464.html

要保证根结点在左孩子和右孩子访问之后才能访问，因此对于任一结点P，先将其入栈。如果P不存在左孩子和右孩子，则可以直接访问它；或者P存在左孩子或者右孩子，但是其左孩子和右孩子都已被访问过了，则同样可以直接访问该结点。若非上述两种情况，则将P的右孩子和左孩子依次入栈，这样就保证了每次取栈顶元素的时候，左孩子在右孩子前面被访问，左孩子和右孩子都在根结点前面被访问。

这个思路很好，目的也是要保证遍历过程的正确性，多使用了一个指针pre来存储前一次访问的节点，这样就可以判断此节点的右子树有没有被访问过。判断条件中

1
(pre!=NULL &&(pre==cur->left||pre==cur->right))

很难理解，一开始会想，这里的pre==cur->left是错误的，因为如果我前一个访问的是该节点的左孩子，那就可以直接访问该节点吗，怎么可能呢。仔细想，就是这样的。因为这种情况只可能出现在，该节点没有右孩子，所以上一个访问完左孩子，直接就可以访问该节点。如果有右孩子在，上一个访问的节点不可能是左孩子，因为右孩子是在此节点之后打入栈中的，会更早的出现在栈顶。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Stack<TreeNode> stk = new Stack<>();
        if(root == null)
            return ans;
        TreeNode curr = root;
        TreeNode prev = null;
        stk.push(curr);
        while(!stk.isEmpty())
        {
            curr = stk.peek();
            if((curr.left == null && curr.right == null) || (prev != null && (prev == curr.left || prev == curr.right)))
            {
                ans.add(curr.val);
                stk.pop();
                prev = curr;
            }
            else
            {
                if(curr.right != null)
                    stk.push(curr.right);
                if(curr.left != null)
                    stk.push(curr.left);
            }
        }
        return ans;
    }
}